Binary Search
Context
Our story begins as all good stories do - with an array. Okay, maybe not all good stories - but certainly all good stories about arrays. Let's take for granted that this array is sorted for now.
Suppose we want to find a particular element in this array, or rather, suppose we want to tell our computer how to find it. What can we do?
The easiest thing to do would be to iterate over the array starting from the beginning and going element-by-element until we find the one we want. This is a pretty good approach actually, and if the array is small, it's probably good enough.
> "Needle is at index 5 in the haystack."
The problem with this approach, however, is that the amount of operations we need to perform grows linearly with the amount of items in our array. Let's say we have an array with 1,000,000 items in it, and the element we're looking for is the very last element in that array. We will need to perform approximately 1,000,000 operations before we find the item we're looking for.
That's where binary search comes in.
The Algorithm
Suppose we have a haystack (a sorted array) and a needle (a specific element that may or may not be in the array), and we want to know where our needle resides in the haystack. In other words - return the index of the needle in the haystack. The binary search algorithm goes as follows:
-
Check middle element of haystack
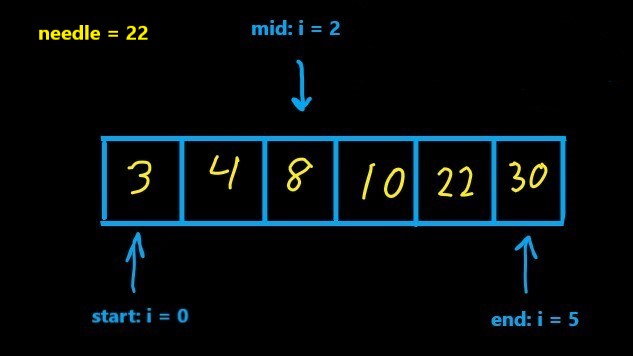
Middle Element -
If the middle element is our needle, return the index - we're done.
-
If the middle element is larger than our needle, remove the right-hand side of the array, if the middle element is smaller than our needle, remove the left-hand side of the array.
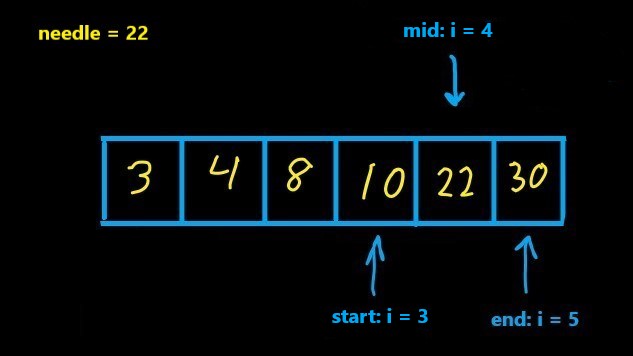
Right half of array -
Repeat steps 1-3 until we find our needle or our array contains only 1 element.
Note that the haystack array must be sorted, or else our algorithm will not work properly.
The Code
Iterative
Recursive
Complexity Characteristics
If you're keeping score on the example, you'll notice that binary search got us down from checking 5 numbers to checking 2. That's pretty good! Alright, so with modern computing power you'll never notice the difference between checking 5 or 2 numbers of a 6 element array. However, when this really starts to matter is when we get into huge arrays.
Recall the hypothetical 1,000,000 element array from before. If we were to take the iterative approach and check every element of the array starting at the first one, in the worst-case scenario we would have to check 1,000,000 elements - that's O(n).
If we take that same 1,000,000 element array (assuming it's sorted) and use binary search to find a certain element, in the worst-case scenario we will check 20 elements. That's because this algorithm has logarithmic complexity - in other words, it is O(log(n)).
You might be wondering, how I got the number 20. Let's dig into that a little bit. The key is in the name of the algorithm - binary search. Essentially, this algorithm is the process of repeatedly slicing an array into two halves and discarding the part we're not interested in.
Take 1,000,000 and divide it by 2 until you get a number less than 1. It will take you 20 times. The intuition for why this works goes like this - imagine each time you divide by 2, you're reducing the number of possible positions the element could be in by half until you reach a single position which will either contain the element or not, at which point you can be sure it was not in the array at all. This is analogous to what happens when you apply log2(1,000,000) which is why this algorithm is considered O(log(n)).